Currently, the use of CSI Safe software version 12.x has become popular in the actual design of floor beam structure due to the advantages compared to version 8.x. Due to the deflection of the floor beams influenced by the phenomenon from the variable and shrinkage of concrete, it increases the crack or reduces the bending hardness of the reinforced concrete structure compared to the case of elastic calculations (with the non -cracked section) leading to increased deflection. In CSI Safe V12.X software, this effect through 2 input parameters:
(See more Part 1)
– CREEP COEFFICIENT: The magnetic coefficient
– Shrinkage Strain: The relative deformation of concrete due to shrinkage

These parameters can be determined according to Vietnamese standards TCVN 5574: 2018, or foreign standardsStructural designReinforced concrete like ACI 318 or Eurocode 2. Here would like to present how to determine these two parameters according to Eurocode 2 (EN 1992: 2004) because this code presents the formula that is easy to determine in practice.
According to the Annex B Appendix of EN 1992: 2004 Part 1-1: General construction design principles and the principle of designing reinforced concrete structure for houses and works.
The coefficient from the Creep Cofficient variable variable is symbolized as $\varphi (t, t_o) $ and is determined by the formula:
$$\varphi_o=\varphi_{RH}\beta(f_{cm})\beta(t_o)$$
where:
$\varphi_o $ is the coefficient from the assumption and is determined at $$\varphi_o =\varphi_ {rh}\beta (f_ {cm})\beta (t_o) $$
$\varphi_ {rh} $ is the coefficient considering the effect of relative humidity on the coefficient from the assumption:
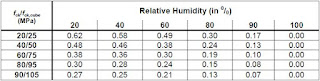
$\varphi_{RH}=1+\frac{1-RH/100}{0,1\sqrt[3]{h_o}}$ with $f_ {cm}\le35MPa $
$\varphi_{RH}=\left[1+\frac{1-RH/100}{0,1\sqrt[3]{h_o}}\alpha_1\right]\alpha_2$ with $f_{cm}>35MPa$
Rh is the moisture of the environment (air humidity), %
$\beta (f_ {cm}) $ is the coefficient for the effect of concrete intensity on the coefficient from the assumption:
$$\beta(f_{cm})=\frac{16,8}{\sqrt{f_{cm}}}$$
$f_ {cm} $ is the average compressive strength of concrete at the age of 28 days, MPA.
To facilitate the design engineers, it is possible to determine $f_ {cm} $ from the concrete mark according to the code TCVN 5597: 1991 (old) as follows:
Characteristic intensity of compressive cube samples: $r_ {ch} = m (1-1,64\upsilon) $
According to TCVN 5574: 2012, the coefficient of assessment of the homogeneity of $\upsilon= 0.135 $ with the current construction condition: There is strict inspection of the composition of concrete and construction quality.
Converted to the characteristic intensity of compressive concrete cylinder: $f_ {ck} = r_ {ch} / 1.25 $
The average compression intensity according to En 1992 is determined by $f_ {cm} = f_ {ck}+ 8 $ (MPa)
$\beta (t_o) $ is the coefficient of the effect of concrete age on the coefficient from the assumption, calculation according to:
$$\\beta(t_o)=\frac{1}{(0,1+t^{0,2}_o)}$$
$h_o $ is the conventional size of the bending (floor) structure, in the unit of MM according to the formula:
$$h_o = \frac {2A_c} {U} $$
$A_C $ is the area of the structure
$U $ is the circumference of the cross -sectional section of the climate with the above moisture.
Usually with $h_o $ = floor thickness
$\beta_c (t, t_o) $ is the coefficient describing the increase of deformation from time variable over time after the load, calculated according to the following formula:
$$\beta_c(t,t_o)=\left[\frac{t-t_o}{\beta_H+t-t_o}\right]^{0,3}$$
$T $ is the time to calculate the deflection (unit: Date), usually long -term consideration at the 5 -year period after the load is deformed from the variable has reached most of its value.
$t_o $ is the age of concrete at the time of waste, usually $t_o = $ 28 days
$\beta_h $ is the coefficient depending on the moisture RH (%) and the conventional size of the structure (Ho by mm) according to the following formula:
$\beta_H=1,5\left[1+(0,012RH)^{18}\right]h_o+250\le1500$ when $f_{cm}\le35$MPa
$\beta_H=1,5\left[1+(0,012RH)^{18}\right]h_o+250\alpha_3\le1500\alpha_3$ when $f_{cm}>35$MPa
$\alpha_ {1,2,3} $ are the coefficients that include the effect of concrete intensity:
$$\alpha_1=\left[\frac{35}{f_{cm}}\right]^{0,7}, \alpha_2=\left[\frac{35}{f_{cm}}\right]^{0,2}, \alpha_3=\left[\frac{35}{f_{cm}}\right]^{0,5}$$
According to Section 3.1.4 (5) of En 1992: 2004 code, shrinkage deformity $\varepsilon_{cs}$ of concrete is made up of two components: $\varepsilon_ {CD} $ and shrinkage due to $\varepsilon_ {ca} $.
Deformation due to slightly shrinkage grows slowly, depending on the osmosis of water through the concrete block. Shrinking deformation developed by Ninh during the concrete bonding process, so most of them take a few days after the concrete. Snacking and shrinkage is the most functional function according to the concrete intensity and should be particularly important in the case of new concrete reflections adjacent to the concrete concrete.
The value of shrinkage strain due to drying over time is calculated by the formula:
$$\varepsilon_{cd}(t)=\beta_{ds}(t,t_s)k_h\varepsilon_{cd,0}$$
$$\beta_{ds}(t,t_s)=\frac{t-t_s}{t-t_s+0,04\sqrt{h_o^3}}$$
$t_s $ is the time when the concrete begins to be deformed dry, usually the end of concrete nursing: 3 days.
$k_h $ is the factor depending on the conventional size of $ h_o $ of the structure according to the following table:

In which: $$\varepsilon_{ca}(\infty)=2,5(f_{ck}-10).10^{-6}$$
$$\beta_{as}(t)=1-e^{-0,2t^{0,5}}$$
Thus, the input parameters to calculate the deflection with Safe software are full for construction design. To facilitate the design engineers in practice, I would like to send the Excel file theme to calculate the parameters of CREEP COEFICIENT and Shrinkage Strain according to Eurocode 2 standards here.

